Puede que necesites conocer el punto donde se cortan dos rectas en un plano, para ello ahora dispones de una función que te permitirá calcular ese punto, tanto si se cortan físicamente o viendo si la proyección de los puntos que determinan las rectas se cortan en el espacio. La función asume que los puntos están siempre en el mismo plano.
También incluimos dos funciones que identifican si las líneas que determinan cada una de las dos rectas es una línea horizontal o vertical, con ello abreviamos la obtención del punto de intersección sin entrar en el cálculo.
A continuación el código de las funciones:
/// <summary>
/// Comprueba si dos puntos definen una línea horizontal
/// </summary>
/// <param name=”p1“>Primer punto</param>
/// <param name=”p2“>Segundo punto</param>
/// <param name=”precision“>Precisión decimal</param>
/// <returns>True o False en función de si es horizontal o no</returns>
public static bool IsHor(Point3D p1, Point3D p2, short precision = 2)
{
if (Trunk(p1.y, precision) == Trunk(p2.y, precision))
{
return true;
}
return false;
}
/// <summary>
/// Comprueba si dos puntos definen una línea vertical
/// </summary>
/// <param name=”p1“>Primer punto</param>
/// <param name=”p2“>Segundo punto</param>
/// <param name=”precision“>Precisión decimal</param>
/// <returns>True o False en función de si es vertical o no</returns>
public static bool IsVer(Point3D p1, Point3D p2, short precision = 2)
{
if (Trunk(p1.x, precision) == Trunk(p2.x, precision))
{
return true;
}
return false;
}
/// <summary>
/// Obtiene la intersección de dos rectas definidas por cuatro puntos
/// </summary>
/// <param name=”v1“>Línea 1. Punto inicial</param>
/// <param name=”v2“>Línea 1. Punto final</param>
/// <param name=”v3“>Línea 2. Punto incial</param>
/// <param name=”v4“>Línea 2. Punto final</param>
/// <param name=”ExtensAll“>Especifica si hay que calcular la intersección sobre la
/// proyección de las dos líneas o sobre los propios segmentos de línea</param>
/// <param name=”precision“>Precisión decimal</param>
/// <returns>El punto de intersección o null si no hay intersección</returns>
public static Point3D Inters2D(Point3D v1, Point3D v2, Point3D v3, Point3D v4,
bool ExtensAll = false, short precision = 2)
{
Point3D pt;
try
{
// Comprueba si son perpendiculares – a->b
if (IsHor(v1, v2, precision) && IsVer(v3, v4, precision))
{
pt = new Point3D(v3.x, v1.y, 0);
if (ExtensAll)
{
return pt;
}
else
{
if (PointInLine(pt, v1, v2, precision) && PointInLine(pt, v3, v4, precision))
{
return pt;
}
else
{
return null;
}
}
}
// Comprueba si son perpendiculares – b->a
if (IsVer(v1, v2, precision) && IsHor(v3, v4, precision))
{
pt = new Point3D(v1.x, v3.y, 0);
if (ExtensAll)
{
return pt;
}
else
{
if (PointInLine(pt, v3, v4, precision) && PointInLine(pt, v1, v2, precision))
{
return pt;
}
else
{
return null;
}
}
}
// No hay relación de perpendicularidad
// Verificar si hay coincidencias por los puntos finales de los segmentos
if (v1.Equals(v3) || v1.Equals(v4))
{
return v1;
}
if (v2.Equals(v3) || v2.Equals(v4))
{
return v2;
}
// No hay coincidencias por los puntos finales
// Aplicar fórmulas.
double NumA = ((v4.x – v3.x) * (v1.y – v3.y)) – ((v4.y – v3.y) * (v1.x – v3.x));
double DenA = ((v4.y – v3.y) * (v2.x – v1.x)) – ((v4.x – v3.x) * (v2.y – v1.y));
double NumB = ((v2.x – v1.x) * (v1.y – v3.y)) – ((v2.y – v1.y) * (v1.x – v3.x));
double DenB = ((v4.x – v3.x) * (v2.x – v1.x)) – ((v4.x – v3.x) * (v2.y – v1.y));
double Ua = 0;
double Ub = 0;
double x = 0;
double y = 0;
if (NumA != 0 && DenA != 0)
Ua = NumA / DenA;
if (NumB != 0 && DenB != 0)
Ub = NumB / DenB;
if (DenA == 0 && DenB == 0)
return null;
if (DenA != 0)
{
x = v1.x + (Ua * (v2.x – v1.x));
y = v1.y + (Ua * (v2.y – v1.y));
}
else if (DenB != 0)
{
x = v3.x + (Ub * (v4.x – v3.x));
y = v3.y + (Ub * (v4.y – v3.y));
}
else
return null;
pt = new Point3D(x, y, 0); // Punto teórico de intersección.
if (ExtensAll)
{
return pt;
}
else
{
if (PointInLine(pt, v3, v4, precision) && PointInLine(pt, v1, v2, precision))
{
return pt;
}
else
{
return null;
}
}
}
catch (Exception ex)
{
MessageBox.Show(“Error:” + Environment.NewLine + ex.Message, “Test”,
MessageBoxButtons.OK, MessageBoxIcon.Error);
return null;
}
}
Para ponerlo a prueba puedes escribir un método parecido al siguiente:
private void intersecciónToolStripMenuItem_Click(object sender, EventArgs e)
{
// Caso 1. Dos perpendiculares horizontal y vertical
Point3D p1 = new Point3D(0, 100, 0);
Point3D p2 = new Point3D(100, 100, 0);
Point3D p3 = new Point3D(50, 0, 0);
Point3D p4 = new Point3D(50, 200, 0);
Point3D result = MyClase.Inters2D(p1, p2, p3, p4, false, 2);
if (result == null)
{
MessageBox.Show(“No hay intersección”, “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
else
{
MessageBox.Show(result.ToString(), “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
p1 = new Point3D(0, 120, 0);
p2 = new Point3D(100, 90, 0);
p3 = new Point3D(40, 0, 0);
p4 = new Point3D(60, 200, 0);
result = MyClase.Inters2D(p1, p2, p3, p4, false, 2);
if (result == null)
{
MessageBox.Show(“No hay intersección”, “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
else
{
MessageBox.Show(result.ToString(), “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
p1 = new Point3D(0, 120, 0);
p2 = new Point3D(100, 90, 0);
p3 = new Point3D(40, 0, 0);
p4 = new Point3D(95.3745, 44.0976, 0);
result = MyClase.Inters2D(p1, p2, p3, p4, false, 2);
if (result == null)
{
MessageBox.Show(“No hay intersección”, “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
else
{
MessageBox.Show(result.ToString(), “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
p1 = new Point3D(0, 120, 0);
p2 = new Point3D(100, 90, 0);
p3 = new Point3D(40, 0, 0);
p4 = new Point3D(95.3745, 44.0976, 0);
result = MyClase.Inters2D(p1, p2, p3, p4, true, 2);
if (result == null)
{
MessageBox.Show(“No hay intersección”, “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
else
{
MessageBox.Show(result.ToString(), “Test”, MessageBoxButtons.OK, MessageBoxIcon.Information);
}
}
Si todo ha ido bien deberías obtener unos resultados parecidos a los siguientes:
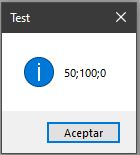
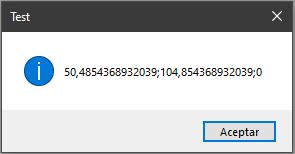
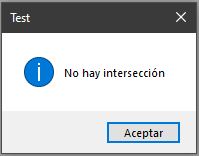
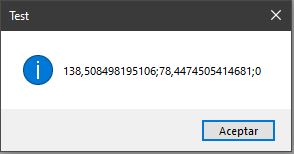
Ponlo a prueba, piensa en cómo mejorarlo y comparte con nosotros tus progresos.

